By Carl Sigmond, Senior, Central High School, Philadelphia, PA
Printed in: Spark!, Key Curriculum Press, Emeryville, CA, Fall 2009.
I was first introduced to The Geometer’s Sketchpad in the summer of 2002 when my mother and were vacationing at a friend’s house. Being math junkies, we sat down one evening to sketch a Star of David fractal. Noticing this, our friend told us that he could make the fractal on his computer and beckoned me to come watch. I was transfixed as he constructed the line segments and connected the points to make the repeating image. I had no idea that this piece of software would enable me to construct hundreds of complex sketches over the next seven years and teach me numerous algebraic and geometric concepts that would prepare me for my high school math curriculum.
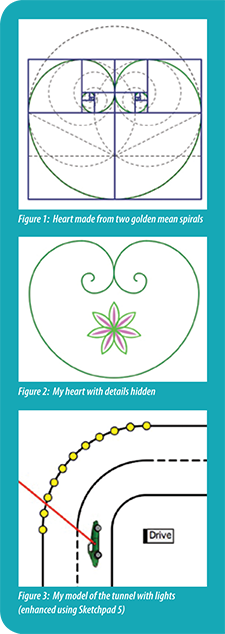 When I got my own copy of Sketchpad, I quickly learned its tools and functions. I then began to create simple designs and marveled at the example scripts that were included in the software package. How can anyone do that, I remember thinking as I watched a car with square wheels roll across the screen. After a short time, I moved from the novice user to the advanced one-creating golden mean spirals and flowers with odd numbers of petals. My favorite sketch from that time period is a heart made from two golden mean spirals. Just for fun, I threw in a seven-petaled flower in the center of the heart. This sketch is pictured here with detail shown and hidden (Figures 1 and 2).
When I got my own copy of Sketchpad, I quickly learned its tools and functions. I then began to create simple designs and marveled at the example scripts that were included in the software package. How can anyone do that, I remember thinking as I watched a car with square wheels roll across the screen. After a short time, I moved from the novice user to the advanced one-creating golden mean spirals and flowers with odd numbers of petals. My favorite sketch from that time period is a heart made from two golden mean spirals. Just for fun, I threw in a seven-petaled flower in the center of the heart. This sketch is pictured here with detail shown and hidden (Figures 1 and 2).
As I grew older, I began to sketch scenarios that I observed in my daily life. One day I was in the car driving towards our local airport when I noticed a peculiar phenomenon. We were about to enter a tunnel that curved 90 degrees. As we approached the tunnel, the rate at which the lights on the outside of the tunnel disappeared behind a concrete wall increased rapidly. I went home, opened my computer, and created the tunnel, the lights, and the car on Sketchpad. It was obvious from the sketch that the rate was increasing while the car’s speed remained constant, but I did not know why. When I showed this sketch to a friend who had a greater knowledge of math than I did, we explored the trigonometry of the situation. At what angle was the passenger looking at each light before the light disappeared? How fast and why was the rate increasing? These are the types of questions that arise and can be answered with Sketchpad. The tunnel sketch is enhanced using Sketchpad Version 5 (Figure 3).
The black horizontal and vertical lines represent the roadway, and the black arcs represent the tunnel. The yellow points on the biggest arc represent the lights. The red line coming out of the car is my line of vision. (I cannot see to the right of the red line because the middle arc is the concrete wall. In the dynamic version of the sketch, the car starts farther down the road and then drives towards the tunnel at a constant rate.
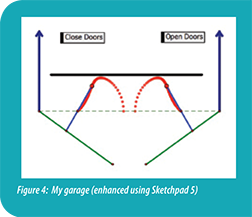 Another scenario that intrigued me was literally in my own backyard. I have a garage that has two doors that swing outwards. A brace connects the top of each door to the doorframe. As is shown in my sketch, the ends of the two braces are fixed to points on each door, but the braces are able to slide through the connection points on the frame. When the doors are opened and closed, the other ends of the two braces make a curious shape in space. The act of opening and closing the doors causes the braces to move away from the doorframe. They seem like they will collide with a pipe that is on the ceiling of my garage, but, at the last minute, they switch directions and return to the doorframe. I went inside and developed a model of my garage on Sketchpad. When I traced the points at the ends of the braces, I clearly saw the paths that they make in space (Figure 4).
Another scenario that intrigued me was literally in my own backyard. I have a garage that has two doors that swing outwards. A brace connects the top of each door to the doorframe. As is shown in my sketch, the ends of the two braces are fixed to points on each door, but the braces are able to slide through the connection points on the frame. When the doors are opened and closed, the other ends of the two braces make a curious shape in space. The act of opening and closing the doors causes the braces to move away from the doorframe. They seem like they will collide with a pipe that is on the ceiling of my garage, but, at the last minute, they switch directions and return to the doorframe. I went inside and developed a model of my garage on Sketchpad. When I traced the points at the ends of the braces, I clearly saw the paths that they make in space (Figure 4).
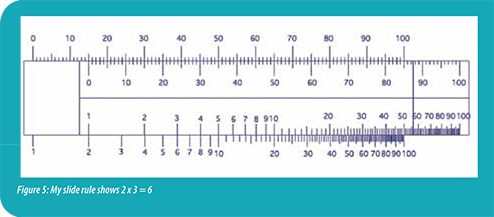
Time passed, and I would use Sketchpad to draw colorful pictures, make fancy animations, and ponder over geometric problems. I then constructed a slide rule. Inspired by my grandfather’s complex slide rule that he used in his college days, I made the addition/subtraction and multiplication/division scales on Sketchpad. The addition/subtraction scales were easy because they have fixed units, but to do multiplication/division, logarithmic scales are necessary. No problem – Sketchpad can calculate logs! When the sketch was complete, I remember noticing the similarities among the four basic arithmetic functions. The methods used for multiplication and division were the same for addition and subtraction. In the dynamic version of the sketch, I can drag one set of scales emulating a traditional slide rule (Figure 5).
It was only after I entered high school that I realized what Sketchpad had done for me. While I constructed the line segments that make up the golden mean rectangle or the arcs that represented the tunnel near my airport, I was learning math. When I started my sophomore Geometry course, I realized that I knew many of the concepts that were being taught in the Discovering Geometry curriculum. I knew how to construct a perpendicular bisector and what an iteration was. I knew how to translate, rotate, dilate, and reflect objects. Throughout that year, I used my knowledge of Sketchpad to explore, investigate, and question the concepts that I was now officially learning in the classroom. In the subsequent Algebra 2, Precalculus, and Calculus courses that I took in high school, I continued to use Sketchpad to help process and visualize the concepts that I was learning. Sketchpad is a great tool for learning and enjoying mathematics.